Note: For groups that have a significant amount of programming experience, your PM may suggest trying out the Advanced Tutorial 6

Submitting

Regardless of how you choose to complete the assignment, you MUST submit the file you worked on to Canvas.

If you’re submitting remotely, your submitted file will be graded for completeness and correctness via an autograder. Make sure your functions are named correctly and that all of the built-in check-expects pass.

If you’re submitting in-class, make sure to check-in (there will be one question called CHECK-IN Q only available for the first 7 minutes of class) and check-out (there will be a three questions survey called CHECKOUT SURVEY only available for the last 10 minutes of class) using PollEverywhere with your location verified.

Getting Started

In this tutorial, we’ll practice working with recursion on linked structures such as lists and trees.

Tutorial 6 Starter Files

Part 1. drop

Write a function (drop a-list k) that returns a copy of a-list with the first k elements removed. In other words, if we ran

(drop '("a" "b" "c") 2)

we’d get back the one element list '("c").

Note that you won’t need to use cons for this, just rest as we’re removing elements from a list not building a new one.

Here’s some help to get you started:

Part 2. take

Now write a function (take list k) that returns a list of just the first k elements of the inputted list. In other words,

(take '("a" "b" "c") 2)

should return the two element list '("a" "b"). Note that you’ll need to use both rest (to remove elements) and cons (to build a new list) for this. Use the same method as above.

Inductive data structures

We talked in the linked list lecture about how lists can be built from simpler structures called pairs. Each pair has a single element and a link to the next pair, which has a single element and a link to the pair after that, …, and so on until eventually the last pair lists the next pair as the empty list, usually notated as '(). This allows us to use a very succinct definition for a list:

Definition: A list is either:

  • '() or
  • (cons e a-list) where e is an element of a-list and a-list is some list.

This is called an inductive definition, or sometimes a recursive definition. Based on this definition, we know that lists include:

And so on. As we discussed, when we type (list 3 2 1) or '(3 2 1), we’re really just getting (cons 3 (cons 2 (cons 1 '()))). The quote notation is just a convenient shorthand.

Trees

Now let’s talk about a different inductively defined data structure called a tree. Trees are used to represent some kind of hierarchy and are best introduced by an example. When we list a taxonomy of something:

Taxonomy Tree

We structure it as a set of items, like “living thing,” “plant,” “animal”, etc., together with lines indicating what is a “subclass” of what. This kind of branching structure is called a tree. The different items are called nodes of the tree and their connections or branches group them into a hierarchy. The top of the hierarchy (“living thing”) is called the root, and the things beneath it and connected to it (“plant” and “animal”) are called its children. They, in turn, can have children (and so on and so on). In this case, “plant” has the children “herbaceous” and “woody”. At the bottom of the hierarchy are items that don’t have any children, which are called leaves. The leaves here are “herbaceous”, “word”, “fish”, “lizard”, “bird”, and “mammal”.

Tree are absolutely ubiquitous in computing and are a powerful example of an inductive or recursive data structure. The folders on your hard drive form a tree, for example. Because trees are defined recursively, many of the functions we use to work with trees are themselves recursive. This is one of many reasons why recursion is a powerful programming tool to have in your toolkit.

Of course, as with anything, there are different flavors of trees. One such important type of tree is a binary tree. That simply means a tree in which nodes aren’t allowed to have more than two children. So when the tree splits, it never splits more than two ways. Here’s a set of numbers arranged in a binary tree:

Example Binary Tree

In Racket, we can easily define a binary tree of numbers inductively, the same way we defined lists inductively. First, we need to define a struct to represent nodes that branch:

(define-struct branch (number left right))

This says that a branch object has a number and a left and right child. Of course, some nodes are just numbers. You make a branch object by saying (make-branch number left right) where number is the number you want to store in the node and left and right are its children.

Given that, we can inductively define a binary tree of numbers as follows:

Definition: A binary-tree is either:

  • a number, or
  • (make-branch number binary-tree binary-tree)

Given this definition, we can say the following are all valid binary trees:

This definition also gives us a way to write recursive functions on binary trees. Since we know a tree is always either a number or a branch (that contains further trees inside it), we can have our base case be when the tree is just a single number (which we can test using the number? predicate) and our recursive case be when it’s a branch (in which case we recurse on the left and right children).

Part 3. Making a Tree in Racket

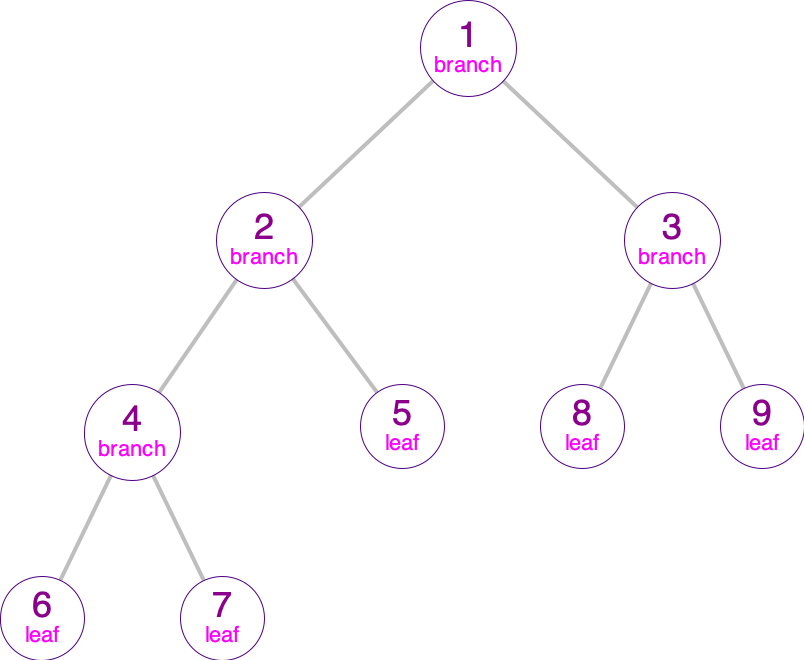
The numerical binary tree above would look like this in Racket:

(make-branch 1
             (make-branch 2
                          (make-branch 4 6 7)
                          5)
             (make-branch 3 8 9))

This says that 1 is the root of the tree, but with two branches. Its branches are 2 and 3, both of which also have branches. 2 branches into 4 and 5, where 4 branches into 6 and 7, but 5 doesn’t branch (it’s a leaf). And 3 branches into 8 and 9 that are both leaves.

Note: We have provided a function, draw-binary-tree, for visualizing binary trees. For example, this visualizes the numerical binary tree above:

(draw-binary-tree
 (make-branch 1
       (make-branch 2
                    (make-branch 4 6 7)
                    5)
       (make-branch 3 8 9)))

Make sure to define this tree in your .rkt file so you can use it as a complex test structure for the next 2 problems.

Now, fill in the definitions of the numerical binary trees that look like the given image.

  1. The tree tree-a should look like: A one-element binary tree
  2. The tree tree-b should look like: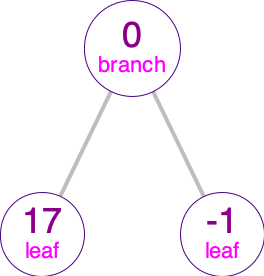 A binary tree containing 0, 17, and -1
  3. The tree tree-c should look like: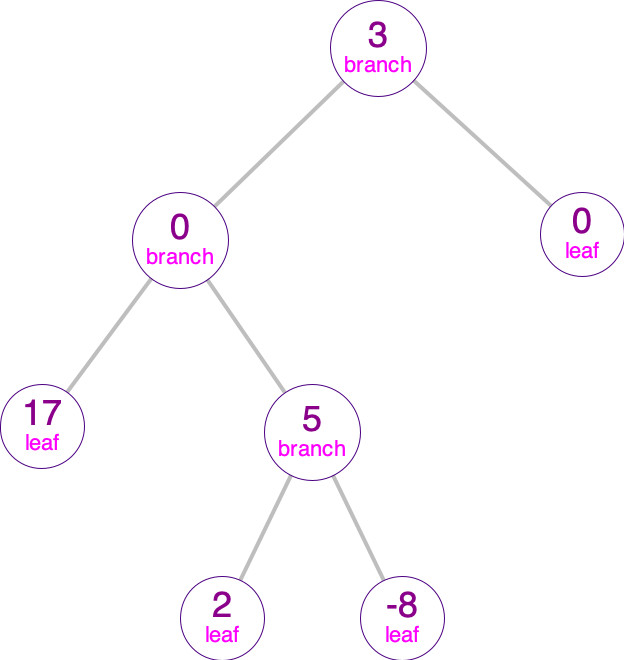 A binary tree that contains 7 numbers

Part 4. count-tree

Write a recursive function, count-tree, that counts the number of numbers in a binary tree.

count-tree : BinaryTree -> Number

If a number appears twice, count both occurrences. That is,

(count-tree (make-branch 1
                         (make-branch 2 0 0)
                         (make-branch 3 0 4)))

should return 7, in spite of 0 appearing three times.

However, (count-tree 0) should just return 1 (since the only number in that tree is 0).

Here’s some subgoals to help you get started:

Hint: this is a tree, so it’s probably tree recursion, right? So we’re probably calling ourselves twice and combining the answers!

Part 5. sum-tree

Write a recursive function, sum-tree, that sums all the numbers in a binary tree.

sum-tree : BinaryTree -> number

For instance,

(sum-tree (make-branch 1
                       (make-branch 2 0 0)
                       (make-branch 3 0 4)))

should return 10. But (sum-tree 3) should just return 3. Again, here’s some steps to get you started: